Tilbage til Startside
Fire metoder viser bopladser
fra yngre stenalder og ældre bronzealder.
Modellerne er inddelt i "Lav" (rød), "Middel" (Gul),
"Høj" (Grøn) og "Meget høj"
(Mørkegrøn) sandsynlighed for fund.
Bemærk, at disse
modeller tager udgangspunkt i det samme fundmateriale, og de samme
landskabsvariabler, og at de alligevel er faldet meget forskelligt ud.
Binær addition
Den grundlæggende analyse af fundenes forhold til landskabet
viser, hvilke områder der er foretrukne for bosættelse, og hvilke man
undgår. Ideen i den binære addition er ganske enkelt at omkode
variablerne, sådan at de foretrukne - eller "gode" - områder får værdien
1, mens de "dårlige" områder får værdien 0. Ved at gøre dette for hver variabel fås en serie
binære kort, som adderes. Resultatet kan således ses som et slags
pointsystem over antallet af "gode" variabler i landskabet. Enklere
kan det næsten ikke gøres, men tidligere forsøg har vist, at metoden
rent faktisk fungerer, og næsten forbavsende godt (Stancic & Kvamme
1999; Ejstrud 1999).
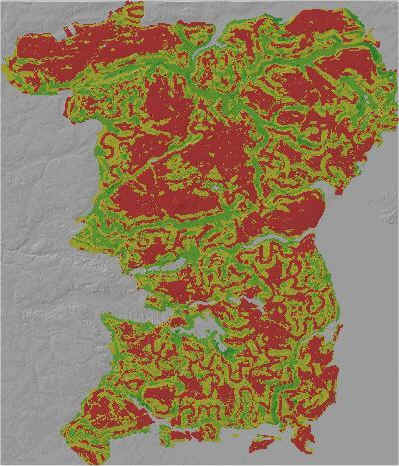
Binær addition
Vægtet binær addition
Omvendt har denne simple metode nogle indlysende
ulemper. Til disse hører, at brugen af værdierne 1 og 0 er en påstand
om, at alle variable er lige vigtige for placeringen af forhistoriske
aktiviteter. Dette er åbenlyst ikke tilfældet, og derfor blev der
udviklet et vægtningsmål, som kunne angive relative forskelle mellem de
forskellige variable.
Grundlaget i denne metode er altså stadig de binære
grundkort over "gode" og "dårlige" steder, men hvert kort vægtes,
sådan at man kan angive et mål for, f.eks. om afstanden til vand betyder
mere end at bosætte sig på den rette jordbund.

Vægtet binær addition
Logistisk regression
Vægtningen ændrer dog ikke på et grundliggende
problem ved den binære klassifikation. Inddelingen i kun "godt" og
"dårligt" giver en meget hård klassifikation, som danner skarpe skel
i landskabet. Det er vanskeligt at forestille sig, at fortidens valg og
fravalg af steder er foregået som tilsvarende skarpe valg.
En løsning er derfor at erstatte det "Ja eller
Nej", som de binære modeller udtrykker, med det udsagn om "Mere eller
Mindre", som sandsynligheds-
baserede modeller benytter sig af.
En internationalt meget populær metode har været
logistisk regression. Den bygger på en sammenligning af placeringen af
dikotome udfald. I dette tilfælde måles altså placeringen af "fund"
i forhold til "ikke-fund", hvor det sidstnævnte er steder, hvor man
ikke har fundet noget.
Som nævnt har metoden været populær. Men allerede
teoretisk må man stille spørgsmålstegn ved den. Udsagnsværdien af en
kategori af "ikke-fund" må anses for meget svag, og metoden kommer
derfor til at bygge på negativt vidnesbyrd snarere end en egentlig
dikotomi.
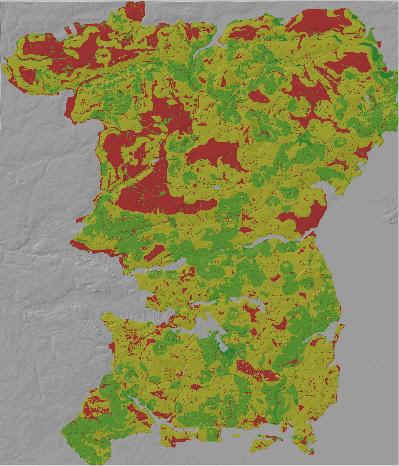
Logistisk regression
Dempster-Shafer teori
Den sandsynlighed, vi vil måle i en indikativ model
er da heller ikke fund i forhold til "ikke-fund". Det drejer sig om at
angive sandsynligheden for fund, målt på et bestemt sæt af
landskabsvariabler, og i forhold til andre sæt af landskabsvariabler.
Denne indfaldsvinkel er benyttet i den sidste metode,
som er anvendt, og som bygger på Dempster-Shafer teori (Eastman 1997).
Beregningerne i denne metode bygger på Bayesiansk statistik, men med den
meget vigtige tilføjelse, at den tager hensyn til manglende eller
ufuldkommen viden. Det gør den særdeles interessant i forbindelse med
empiriske modeller, og ikke blot inden for arkæologien. I en GIS sammenhæng
kan metoden endda beregne og kortlægge graden af uvidenhed, hvilket i
praksis giver et kort over steder, hvor yderligere dataindsamling med størst
fordel kan gennemføres.
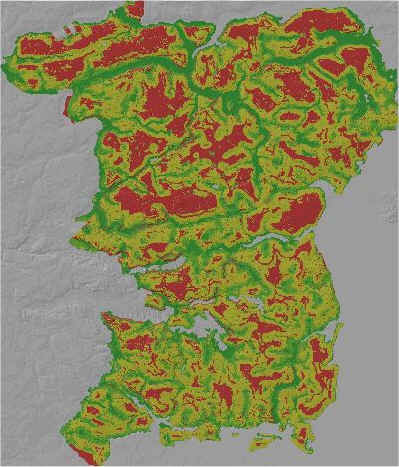
Dempster-Shafer teori
Resultater
Med disse fire metoder er der lavet modeller for seks
hovedkategorier af fund, i alt 24 modeller. For at kunne måle deres
relative effektivitet er der herefter benyttet et mål, "Udbytte", som
på en skala fra 0 til 1 viser, hvor meget bedre modellen er end en helt
tilfældig model (Kvamme 1987). Resultatet er vist på tabellen herunder.
Det ses, at de mest effektive modeller laves med vægtet binær addition
og med Dempster-Shafer modellerne.
Modellerne er ikke sammenlignelige fra fundkategori
til fundkategori, og derfor skal man, på trods af det standardiserede mål,
være varsom med at sammenligne værdierne på tværs af kolonnerne. Dette
må man tage i betragtning ved en vurdering af tabellens sidste kolonne,
som er en beregning af middelværdien af udbyttet. Som en generel
indikator på modellernes effektivitet giver denne værdi dog et rimeligt
bud.
| |
1 |
2 |
3 |
4 |
5 |
6 |
Middel |
| Binær Addition |
0,84 |
0,25 |
0,33 |
0,29 |
0,19 |
0,35 |
0,36 |
| Vægtet binær addition |
0,87 |
0,24 |
0,42 |
0,23 |
0,33 |
0,35 |
0,41 |
| Logistisk regression |
0,68 |
0,17 |
0,24 |
0,37 |
0,09 |
0,18 |
0,29 |
| Dempster-Shafer |
0,83 |
0,48 |
0,26 |
0,48 |
0,33 |
0,42 |
0,53 |
Tabellen viser modellernes "udbytte".
Kolonnerne viser: 1) Mesolitiske bopladser, 2) Bopladser fra neolitikum og
ældre bronzealder, 3) Tragtbægerkulturens grave, 4) Gravhøje, 5)
Bopladser fra yngre bronzealder og ældre jernalder, 6) Grave fra yngre
bronzealder og ældre jernalder. Kolonnen "Middel" viser middelværdien
af de foregående.
Tilbage til At spå om fortiden
Tilbage til Startside
|